由于unity中默认管线自带的参数化天空盒过于丑陋，而HDRP（好想要它的体积云）似乎还是不推荐在手机上使用，于是我们又得开始自己造轮子了。一番搜索之后，很快我们就找到了本次代码搬运的对象：github.com/ebruneton/pr，代码还附带了详细的文档以及论文。

本文不会详细介绍大气散射计算的原理，而只是记录代码搬运过程的笔记。作者很菜，也是从：06.游戏中地形大气和云的渲染(下) | GAMES104-现代游戏引擎：从入门到实践_哔哩哔哩_bilibili 开始了解的，建议在阅读论文前先看视频或者其他zhihu文章了解原理，以读懂原始论文。

一些光学

这里记录一些在阅读代码时碰到疑惑的光学基础知识。

辐射的定义

我知道辐射（Radiance）的量纲为：单位面积单位立体角的功率，但是常常忘记它的物理图像：

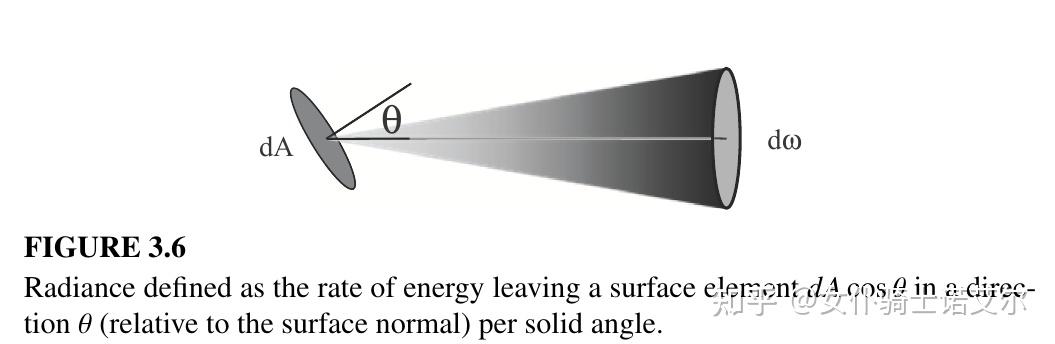
注意此处的立体角是由“观察者ω”的微表面大小决定的。想象此时接收者远离发射源，则收到的功率以面积率（距离的平方反比）衰减，同时立体角也按此规律衰减，则最终计算出的辐射保持不变，或者说因此才要将这个守恒量定义为辐射。人类视网膜感受到的亮度即与辐射相关，而对于屏幕上的像素来说，我们要计算得到的量正是辐射谱（各种波长下的辐射），最终再转化为RGB值由显示器投射出来。

如果忽略功率，仅从几何上来定义这“一束光”，则为光学扩展量（étendue）。

Lambertian BRDF的归一化系数

一个小问题，很容易误认为均匀反射（Lambertian）表面的辐射与辐照度（irradiance）间的系数通过半球面的立体角（2π）关联起来：

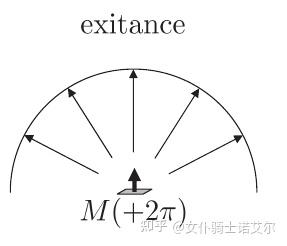
但是参考这个问题，别忘了辐照度的计算需要考虑出/入射光线的角度，乘上系数cos(θ)再进行积分，系数就只剩下π了！

体渲染公式

在介质中的辐射传输有如下图四种散射事件，辐射沿某一方向的微分可以通过各系数加权求得。在计算大气散射的时候，没有自发光（emission），只需要关心衰减（extinction）和内散射（in-scattering）项。注意后两项的辐射L含有下标，需要单独求出，所以in-scattering是最难处理的一项。

in-scattering的辐射量计算需要在散射事件发生的位置x上进行球面积分，其中通过相函数p来描述散射在各种散射夹角下的分布。

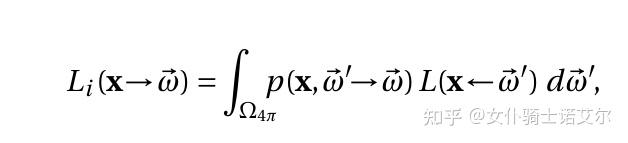
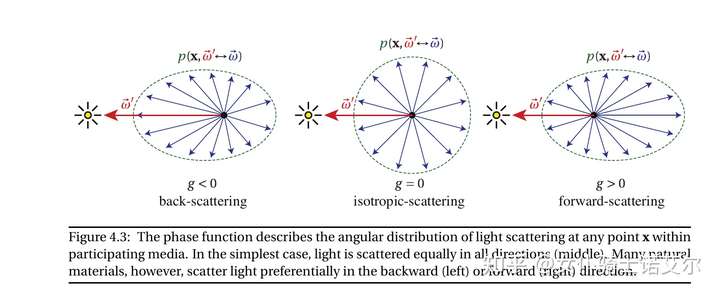
代码阅读

量纲一致性

代码中有个好玩的地方：作者实现了gpu和cpu两种计算方式的算法。其中cpu计算的版本能够通过静态类型检查实现量纲一致性，而代码中的各种物理量都被分配了相应的类型，因此正确性和可读性更好。

在C++版本中，基本单位的定义如下：

typedef dimensional::Angle Angle;
typedef dimensional::Scalar<1, 0, 0, 0, 0> Length;
typedef dimensional::Scalar<0, 1, 0, 0, 0> Wavelength;
typedef dimensional::Scalar<0, 0, 1, 0, 0> SolidAngle;
typedef dimensional::Scalar<0, 0, 0, 1, 0> Power;
typedef dimensional::Scalar<0, 0, 0, 0, 1> LuminousPower;

导出单位则可以通过基本单位组合出来（数值代表了n次幂）：

typedef dimensional::Scalar<2, 0, 0, 0, 0> Area;
typedef dimensional::Scalar<3, 0, 0, 0, 0> Volume;
typedef dimensional::Scalar<-2, 0, 0, 1, 0> Irradiance;
typedef dimensional::Scalar<-2, 0, -1, 1, 0> Radiance;

对于阅读和搬运代码来说，就不用管cpu版本的算法了。在gpu版本中，量纲类型仅起到注释的作用。唯一的缺点就是可能会让强迫症在阅读时总是在纠结量纲的转换和正确性验证。

一点小小的插图欺骗

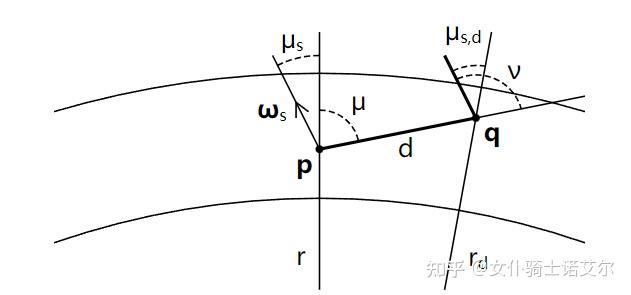
在计算一次散射（的辐射量）时，作者给出了多项乘积，包括各种系数、相函数等，但最关键的是他直接使用了太阳的辐照度irradiance作为一项，同时也没有作球面积分！这和我们上文提到的内散射辐射量公式就不一样了呀。实际上此时是被这个图小小的欺骗了一下，我们依然要计算球面积分，只是在地球上太阳的视角非常小，因此只需要在这一小块立体角中进行积分，同时可以将相函数当作一个常数提到积分外，此时积分内只剩下辐射L了，其结果即为太阳（在大气层外）的辐照度。

$$L_i(\mathbf{x} \rightarrow \vec{\omega}) = p(\mathbf{x}, \vec{\omega_{sun}} \rightarrow \vec{\omega}) \int_{\Omega_{sun}}{L(\mathbf{x} \leftarrow \vec{\omega}') d\vec{\omega}'} \\ L_i(\mathbf{x} \rightarrow \vec{\omega}) = p(\mathbf{x}, \vec{\omega_{sun}} \rightarrow \vec{\omega}) Irrad_{sun} $$

古法预处理器

在具体实现（opengl）中，作者为了避免重复编写vertex/pixel shader，以及在运行时实现类似include的功能，直接采用字符串拼接来生成shader代码的方法。稍微有点接受不能:(

const char kComputeTransmittanceShader[] = R"(
    layout(location = 0) out vec3 transmittance;
    void main() {
      transmittance = ComputeTransmittanceToTopAtmosphereBoundaryTexture(
          ATMOSPHERE, gl_FragCoord.xy);
    })";
// ...
Program compute_transmittance(
        kVertexShader, header + kComputeTransmittanceShader);

unity中的实现

预处理器

为了代码看起来清晰一点，我直接用include命令来替代字符串拼接，并且给每个查找表/贴图的预计算都单独写了一份shader，虽然内容有点重复。

由于没有采用古法预处理器的方法拼接代码，所以实现的版本不支持运行时修改大气的参数，不过对于飞行模拟的场景来说也足够了，只会用到对应于地球大气的默认参数。

GLSL转HLSL

纯粹因为unity官方文档中HLSL使用较多，所以想把代码转成HLSL。由于作者的代码风格很好，转换过程很简单。不过微软给HLSL写的文档真的有点差：单一函数/功能的注释页面还行，可是语言整体设计的完整文档根本找不到，被OpenGL完爆。

转换过程中有几个小问题：

  • const -> static const：怪我没仔细看文档，hlsl里面const只是说在shader不能修改，但也在constant buffers里作为参数，编译时的值是不确定的，需要加上static修饰符才与glsl中的const语义相同。
  • 没有默认构造函数：自定义的类型是没有构造函数的，只能手动对字段赋值。解决的办法是手写一份构造函数:)，名字加个下划线防止重复定义，还好用的地方不多。
  • 缺少部分向量维度隐式转换：这个其实还挺好的，不容易写出隐藏bug，但是修改起来就比较烦人。

天空盒

预计算部分完成后就要进行应用了，最简单的就是将其作为天空盒的材质。好在unity已经内置了天空盒的mesh以及GI的计算，我们只要简单修改一下vertex shader，并将地形遮挡/阴影长度参数直接置为0就可以。

在Android上运行的时候，还发现了作者一个小bug：地平线附近颜色不对，最后发现是某处对负数开平方了，不过在PC上很神奇的无事发生。

对于飞行模拟游戏来说，通常还会使用 浮动原点 技术避免数值精度问题，此时还需要小小地修改一下，将浮动原点的y轴高度也考虑进去，xz轴则无需关心。

成品链接

github：GitHub - beantowel/Aerosol: Precomputed Atmospheric Scattering for unity

Asset store（免费）：Aerosol | 2D Sky | Unity Asset Store