在气动力的计算中，需要获知飞行器所在位置的空气密度来计算动压等参数，因此需要大气模型来计算（不同高度的）空气参数。jsbsim中采用了U.S. Standard Atmosphere, 1976", NASA TM-X-74335 （美国标准大气）模型。

实际应用中不同地区的大气环境不一样（比如海平面温度不同），我们先忽略这个问题，只关注最基本的原理。基本的信息可以在wiki：en.wikipedia.org/wiki/I里查看。

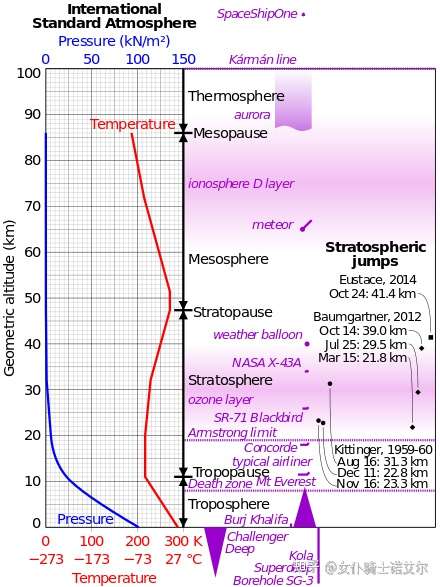
高度

标准大气模型描述了不同高度上大气参数的变化，这里我们需要了解两种高度的定义：geometric altitude（标准高度）和geopotential altitude（势能高度）。前者很简单，就是物体与海平面间的距离；后者考虑了不同高度上重力加速度g的变化，通过g与高度差的积分计算出了重力不变情况下的等效高度，从名字上也能看出来，物体的势能可以直接用这个高度与地表重力加速度、质量相乘获得。

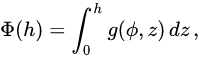
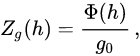
实际应用中不需要计算复杂的积分，可以通过地球半径来计算势能高度，以下是jsbsim中的实现，只需要普通的四则运算即可 ：

温度、压强、密度

在标准模型中，温度基本是随着高度（分段）线性变化的，所以我们可以方便地将这些数据存在表格里，进行插值计算，而其他两个参数则可以通过求解方程获得。

根据流体静力平衡和理想气体模型，有下面两个公式：

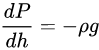
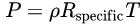
替换变量再化简一下的话就是

$$dlnP = \frac{-g(h)}{R_{spec}T(h)}dh\\ $$

在温度随高度线性变化的分段函数上积分，可以进一步简化：

$$\frac{P_1}{P_0} = \frac{T_0}{T_0+k \Delta h}^{\frac{g_0}{R_{spec} k}}\\$$

其中k是温度直减率（lapse rate）， P_0 为分段函数转折点压强，与转折点间的（势能高度）差为 \Delta h 。通过这个公式与预先计算好的各转折点压强，就能获得各高度上的压强，气体密度亦可以再通过理想气体模型获得。

需要注意的是温度梯度较小的时候上式的k->0，直接进行数值计算不太合适，需要将上式退化为

$$\frac{P_1}{P_0} = e^{\frac{-g_0 \Delta h}{R_{spec}T_0}}\\ $$