上文我们讨论解读了jsbsim的配置文件，现在让我们使用程序来加载这个配置文件，进行计算吧。

一个C#语言的“简易版”jsbsim代码还在开发中：github.com/beantowel/mi 预期后续能够作为一个第三方包供unity开发使用。

xml反序列化

在解析配置文件时，我发现实际上jsbsim提供了一份xml的结构描述文件（schema）：JSBSim.xsd。而且里面也提供了一些注释，可以对上文进行补充。我们使用 .net 提供的程序 xsd.exe 直接来生成 c# 中的类，对配置文件进行反序列化。使用方法也很简单，运行：

xsd JSBSim.xsd /classes

就可以了，但是如果我们直接运行这个命令的话，会发现程序报错，因为这个JSBSim存在group元素的循环引用。如下图中func_group -> product -> func_group 的循环。

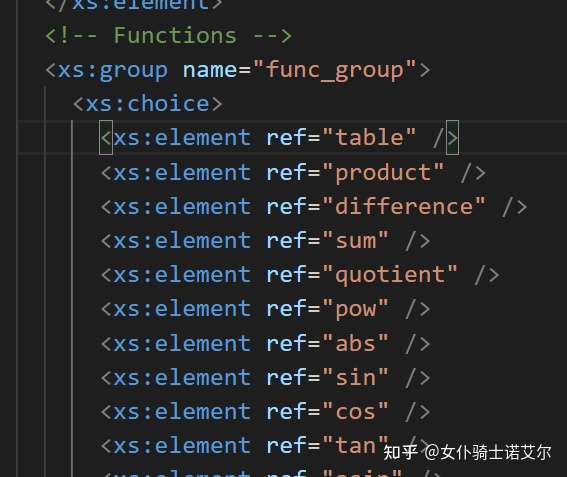
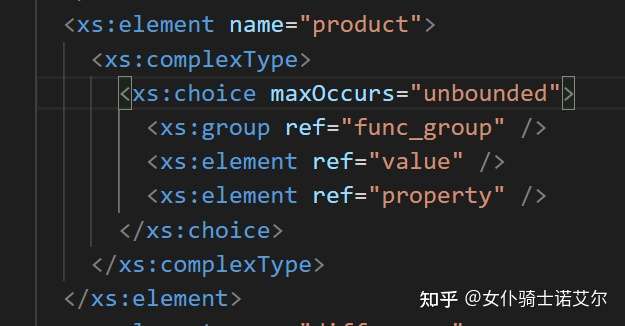
在xsd文件中，我们可以认为 xs:group 类似C语言中的宏命令，在 xsd.exe 程序生成类的过程中是会直接展开的，因此循环引用会导致无穷展开，是非法的。可以参考这个blog来进行一些修改绕过这个限制，具体细节上因为xsd不一样不能直接照搬，我直接把修改后的xsd和生成的class贴在这里。 这样，我们就能对配置文件进行反序列化了。

质量、转动惯量解析

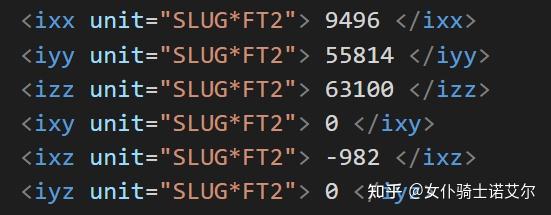
unity仅支持转动张量（惯性主轴主成分构成的Vector3）+ 主轴旋转角格式的输入，即inertiaTensor和inertiaTensorRotation，但是我们的配置文件中给出的是一般的转动惯量形式，因此需要做一下转换。 PhysX 中提供了一个函数PxDiagonalize来对转动惯量进行对角化，可惜我们使用的是c#脚本，无法直接引用c++的库。我尝试过使用PhysX.Net，但是发现里面似乎也没有提供这个方法，并且文档质量太差。最终我还是选择拿c#把c++代码抄一遍完事，简单快捷。

这个算法还挺有趣的，在下面贴一下。主要思路就是通过x，y或z轴的旋转一步步迭代将转动惯量对角化，举个不恰当的例子，就像转魔方一样。区别在于这里的每一步操作都是较优的逼近方程的解，而魔方在我这种菜鸡手上可能永远都转不出来。在这里，m是输入的转动惯量，q是对m的旋转（四元数形式，其对应的旋转矩阵是axes），d=qT m q 是旋转后的转动惯量，迭代的终止条件就是 d 变为对角化矩阵。迭代中我们将每次的x，y或z轴旋转操作累计（累乘）在q上，这里算法的关键就是如何选出我们每次要转的轴，和算出要旋转的角度。

算法选择了惯性积最大的那个轴开刀，即如果Iyz比Ixy、Ixz都大的情况下，优先绕x轴进行调整。 此时要调整的角度phi的余切cot(2 phi)=(Iyy - Izz) / (2 Iyz) ，这个角度就是经过旋转后，能够取得Iyz最小的角度，通过坐标变换和二次函数极值点可以推导出 。

迭代法的收敛性不会证，但是直观上感觉旋转几次基本就够了（注意迭代次数可能大于3次，并不是在每一个轴上旋转一次就足够了，需要来回调整）。代码里设定的最大迭代次数是24次，也说明这个收敛的挺快了。

PX_FOUNDATION_API PxVec3 physx::PxDiagonalize(const PxMat33& m, PxQuat& massFrame)
{
	// jacobi rotation using quaternions (from an idea of Stan Melax, with fix for precision issues)

	const PxU32 MAX_ITERS = 24;

	PxQuat q = PxQuat(PxIdentity);

	PxMat33 d;
	for(PxU32 i = 0; i < MAX_ITERS; i++)
	{
		PxMat33 axes(q);
		d = axes.getTranspose() * m * axes;

		PxReal d0 = PxAbs(d[1][2]), d1 = PxAbs(d[0][2]), d2 = PxAbs(d[0][1]);
		PxU32 a = PxU32(d0 > d1 && d0 > d2 ? 0 : d1 > d2 ? 1 : 2); // rotation axis index, from largest off-diagonal
		// element

		PxU32 a1 = shdfnd::getNextIndex3(a), a2 = shdfnd::getNextIndex3(a1);
		if(d[a1][a2] == 0.0f || PxAbs(d[a1][a1] - d[a2][a2]) > 2e6f * PxAbs(2.0f * d[a1][a2]))
			break;

		PxReal w = (d[a1][a1] - d[a2][a2]) / (2.0f * d[a1][a2]); // cot(2 * phi), where phi is the rotation angle
		PxReal absw = PxAbs(w);

		PxQuat r;
		if(absw > 1000)
			r = indexedRotation(a, 1 / (4 * w), 1.f); // h will be very close to 1, so use small angle approx instead
		else
		{
			PxReal t = 1 / (absw + PxSqrt(w * w + 1)); // absolute value of tan phi
			PxReal h = 1 / PxSqrt(t * t + 1);          // absolute value of cos phi

			PX_ASSERT(h != 1); // |w|<1000 guarantees this with typical IEEE754 machine eps (approx 6e-8)
			r = indexedRotation(a, PxSqrt((1 - h) / 2) * PxSign(w), PxSqrt((1 + h) / 2));
		}

		q = (q * r).getNormalized();
	}

	massFrame = q;
	return PxVec3(d.column0.x, d.column1.y, d.column2.z);
}

空气动力函数解析

jsbsim的配置文件支持了相当多的函数类型，不过在我们选择的f16配置文件中，aerodynamics节点下的子函数只涉及到了product和table两种类型，解析起来比较简单，可以参考文章第一段中提供的代码。

需要注意我们的程序中使用公制单位存储所有数据，property的标识符“node”最后一部分通常会给出单位，便于转换；但是table表格中的数据未给出单位，同时其也可能不是无量纲数，需要额外处理。在f16的配置文件中，所有的表格都最终都是通过product乘法计算出力/力矩的，尚且可以通过其他变量的单位反推其量纲进行处理。

对于Property的处理还没有发现特别好的方案，由于jsbsim采用了这种相当于全局变量的架构，要想使用它的配置文件，我们的组件也必然受到这种设计的影响，这种全局变量的优点是直观、程序设计简单，缺点是对外提供接口语义不清晰、Property间如果有依赖关系容易产生隐形bug。